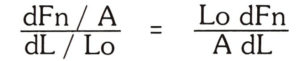Terminology
1. Gage Length: The original length of that portion of the specimen over which strain or change of length is determined.
2. Elongation: The increase in gauge length of a tension test specimen, usually expressed as a percentage of the original gauge length.
3. Stress: The force per unit area that is expressed in pounds per square inch, kilograms per square millimeter, etc.
4. Tensile Stress: Stress which tends to stretch or lengthen the material.
5. Strain (Unit Strain):
a. The amount by which a dimension of a body changes when the body is subjected to a load is divided by the original value of the dimension. The simpler term strain is often used instead of unit strain.
b. A measure of the change, due to force ion the size or shape of a body referred to its original size or shape.
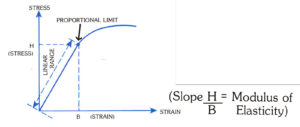
6. Stress-Strain Diagram: A diagram in which corresponding values of stress and strain are plotted against each other. Values of stress are usually plotted as ordinates (vertically) and values of strain as abscissas (horizontally).
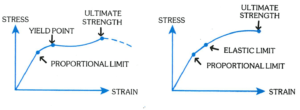
7. Proportional Limit:
a. The point on a stress-strain curve at which it begins to deviate from the straight-line relationship between stress and strain.
b. The greatest stress that a material is capable of sustaining without any deviation from proportionality of stress to strain.
8. Elastic Limit:
a. The maximum stress to which a test specimen may be subject and still return to its original length upon release of load.
b. The greatest stress that a material is capable of sustaining without any permanent strain remaining upon release of the stress.
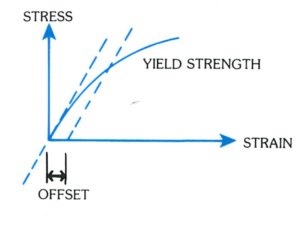
9. Yield Strength: This is the maximum stress that can be applied without permanent deformation of the test specimen.
10. Yield Point:
a. A point on the stress-strain curve at which there is a sudden increase in strain without a corresponding increase in stress.
b. The first point on the stress-strain curve at which an increase in strain occurs without an increase in stress.
11. Ultimate Strength (Tensile Strength): This is the maximum stress value obtained on a stress-strain curve.
12. Offset Method: Because of the difficulty in determining the elastic limit and since many materials do not have an elastic region, yield strength is often determined by the offset method. The yield strength in such a case is the stress value on the stress-strain curve corresponding to a definite amount of permanent set or strain, usually 0.1 or .02 percent of the original dimension.
Modulus of Elasticity
The ratio of stress to corresponding strain without the proportional limit of a material in the tension of compression.
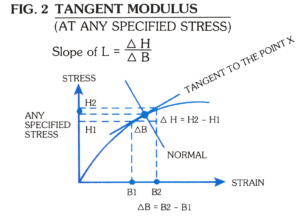
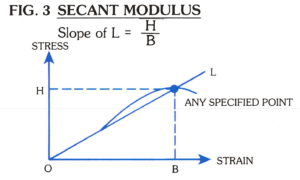
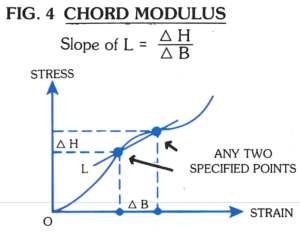
Many materials do not conform to Hook’s Law throughout the elastic range but deviate therefrom even at stresses well below the elastic limit. For such materials, the slope of either the tangent to the stress-strain curve at the origin or at low stress, the secant drew from the origin to any specified point on the stress-strain curve, or the chord connecting any two specified points on the stress-strain curve is usually taken to be the modulus of elasticity.
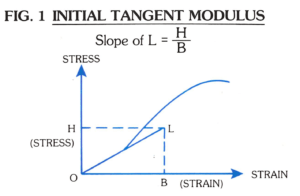
1. Initial Tangent Modulus: The slope of the stress-strain curve at the origin.
2. Tangent Modulus: The slope of the stress-strain curve at any specified stress.
3. Secant Modulus: The slope of the secant drawn from the origin to any specified point on the stress-strain curve.
4. Chord Modulus: The slope of the chord drawn between any two specified points on the stress-strain curve.
If the relation between stress and strain is not linear, an elastic modulus can be defined more generally as the limiting ratio of a small change in stress to the change in strain produced by it. Thus, if the force Fn is increased by dFn, and as a result the length increases by dL, the modulus is defined as:
This is equivalent to defining the modulus at any point as the slope of a curve in a stress-strain diagram.
The slope of the strain line within the proportional limit is the Modulus of Elasticity (or Young’s Modulus) in this stress-strain diagram.
Units: Since a strain is a pure number, the units of Young’s Modulus are the same as those of stress (force per unit area).